
We're sure, without a doubt, that you know Angry Birds. We're equally sure that you've played it - it's available for purchase on innumerable device platforms, and even for free on Google Chrome and Android, albeit with annoying ads.
And we're pretty certain you're better at it than we are.
Just in case, the basic plot of the game is to knock out a bunch of green pigs by firing flightless birds at them from a catapult.
The birds are angry because the pigs have stolen their eggs, and the pigs are trying to protect themselves by hiding in some remarkably ramshackle structures made of wood, glass, or rock. And that's it really.
Put baldly like that it doesn't seem like much, but in reality it's quite addictive. I think that part of the reason for its addictiveness is that the launching and the flight of the birds seems very natural, the collisions authentic, and the wobbliness of the pigs' constructions real. In other words, the game jives with our knowledge of how the real world works, and so we use our experience of throwing balls and stones to work out how the birds will fly as they're launched from the catapult.
We make judgments about how the momentum of the red bird will be transferred to the planks and sheets of glass from our familiarity with colliding snooker balls.
Exploring velocity
So how did the developers at Rovio, the company that produces Angry Birds, write such realistic interactions into the game?
Get daily insight, inspiration and deals in your inbox
Get the hottest deals available in your inbox plus news, reviews, opinion, analysis and more from the TechRadar team.
It all boils down to some fairly simple algorithms. Let's first take a look at the flight of the red bird (to recap, the red bird acts like a cannon ball: it flies and then crashes into something). We'll take it from the point the bird leaves the catapult: it has a certain velocity at a certain angle. What happens next?
There are two components to the velocity: the vertical and the horizontal. The horizontal component is constant; there are no forces acting on the red bird horizontally (I'm sure that Rovio's programmers ignored the friction due to air resistance).
The vertical component on the other hand is subject to the acceleration due to gravity, g, continually pulling the bird down to Earth. Let's assume that g is roughly 10 meters per second squared, as it is at ground level.
If we say that the vertical velocity is v m/s upwards at the point of launch, then a short time later - let's say 1/10 of a second - the vertical velocity will be (v-1) m/s. (In other words, the reduction in velocity is 1/10 of 10 m/sˆ2.) Another 1/10 of a second later the vertical velocity will be (v-2) m/s, and so on.
At some point, gravity will slow down the vertical velocity to zero, after which point, the vertical velocity becomes negative (in other words, the red bird will accelerate downwards - we defined v to be a velocity upwards). So, in short, the vertical velocity of the red bird will decrease from v to 0 upwards, and then increase from 0 downwards.
The theory of kinematics provides the formula w = v + at for the velocity w at a time t given a constant acceleration a and an initial velocity v.
Go the distance
Now that we understand how the velocity changes with time, what about the distance travelled? Again we have two components: the vertical and the horizontal distance.
The horizontal distance is easy; the distance travelled horizontally is simply the constant horizontal speed component multiplied by the time. Vertically, there are a couple of ways we can simulate this: a step-wise algorithm, or by using the relevant kinematics formula.
Since we're emulating reality on a fairly small screen, the step-wise algorithm will work perfectly well. After all, we're going to be displaying the red bird on the screen at one position and then a very short time later at another to give the illusion of motion.
Let's assume that our 'steps' are 1/10 second apart again, and g has the same value. We'll make the assumption also that the speed at the start of a step is maintained throughout the step (in reality we know that this is an approximation - the speed changes continuously).
Using these assumptions, the distance travelled upwards in the first step is v*1/10, in the second (v-1)*1/10, the third (v-2)*1/10, and so on. Eventually the distance travelled goes negative, in other words, downwards.
Now that we have calculated the distance travelled both vertically and horizontally for each step, we can plot this on the Angry Birds screen and see the parabola we'd expect for the path travelled by the red bird. In fact, the way Rovio displays the parabolic path uses little puffs of 'smoke' at regular intervals as if they were calculating the path in this step-wise manner.
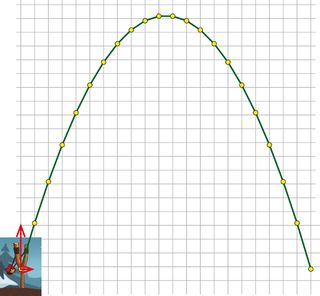
Figure 1 (above) shows this conceptually. In the lower left corner I show the initial components of the velocity in red: a large vertical component (subject to gravity) and a smaller horizontal one (at the start it's roughly in the ratio 3:1). The grid spacing represents the distance travelled horizontally in 1/10 second (you can see that the yellow dots are spaced equally from left to right).
As you can see, the vertical distance travelled gets shorter and shorter upwards every time slice until we reach the top, and then it gets longer and longer downwards. The segments between the yellow dots are all straight; I did not attempt to apply a curve.
For completeness, I'll add the formula from the theory of kinematics to calculate the position q at time t: q = p + v*t + 0.5*a*tˆ2, where p is the initial position, v the initial velocity, and a the constant acceleration. As you can see, this is a quadratic formula in t; that is, a parabolic path.
- 1
- 2
Current page: Angry Birds physics: velocity and distance
Next Page Angry Birds physics: stretching and collisionsMost Popular


